Local Gauss-Bonnet theorem
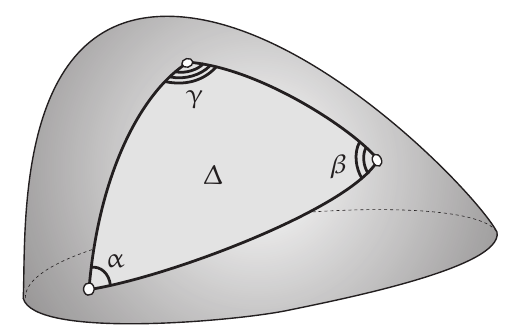
Let $\Delta$ be a geodesic triangle on a surface (pseudo-Riemannian manifold) of dimension 2.
$$ \mathcal{E}(\Delta)=\alpha+\beta+\gamma-\pi=\iint_{\Delta} K \mathrm{d} \mathcal{A} $$where $K$ is the Gaussian curvature.
This theorem says that the angular excess of such a triangle is simply the total curvature inside it.
There is a visual idea of the proof in @needham2021visual page 23:
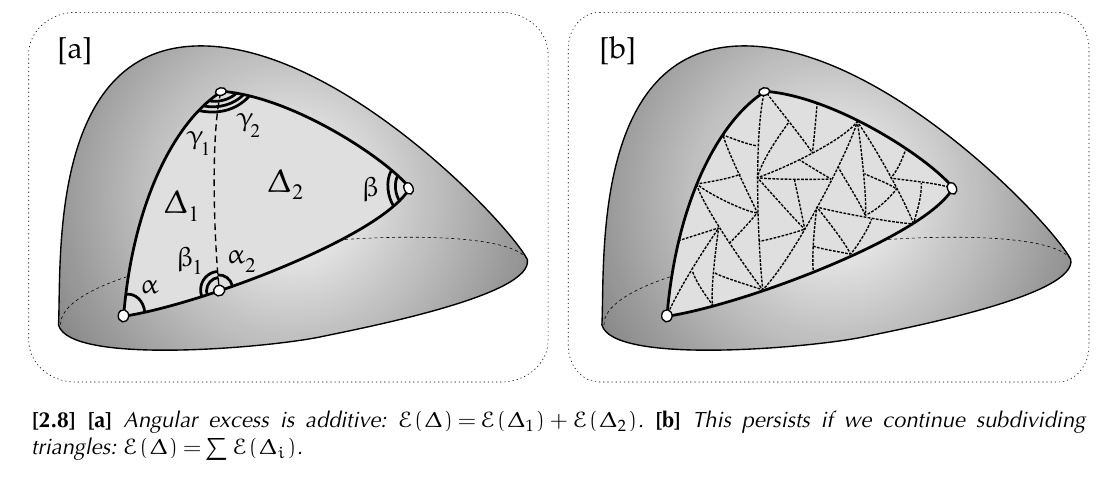
based on the additivity of the angular excess.
It has a surprising global version: global Gauss-Bonnet theorem.
________________________________________
________________________________________
________________________________________
Author of the notes: Antonio J. Pan-Collantes
INDEX: